Sò͘-ha̍k

Sò͘-ha̍k (數學)tiāⁿ hông khoàⁿ-chò sī leh gián-kiù sò͘-liōng, kiat-kò͘, khong-kan kap piàn-tōng ê ha̍k-būn. Ū koá sò͘-ha̍k-ka kā sò͘-ha̍k tòng-chò sī kong-siat kap teng-gī thaù-koè chhui-lūn tit--tio̍h ê tì-sek.
Ta̍k ê siā-hoē leh chhek-liông thó͘-tē, chhú-lí koè-kè, ī-chhek thian-bûn sū-kiāⁿ, ... ê sî chha-put-to lóng ē-tit khoàⁿ tio̍h èng-iōng sò͘-ha̍k ê iáⁿ. Sò͘-ha̍k thong-siông sī leh chhiau-chhoē bô͘-sek, bô tiāⁿ-tio̍h ài kap èng-iōng ū tī-tāi. M̄-koh Eugene Wigner bat kóng koè "sò͘-ha̍k siuⁿ koè-thaû-á ū-haū", siōng 'sûn' ê sò͘-ha̍k tiāⁿ chhoē tio̍h siōng si̍t-chè ê èng-iōng. Hiān-chhú-sî ê chū-jiân kho-ha̍k, kang-têng, keng-chè, i-ha̍k lóng tio̍h khoàⁿ sò͘-ha̍k ū sin hoat-tián--bô.
Hi-lia̍p-gí ê μάθημα (máthema) piáu-sī "kho-ha̍k, tì-sek, ha̍k-si̍p", μαθηματικός (mathematikós) piáu-sī "kah-ì o̍h mi̍h-kiāⁿ". Eng-gí kā sò͘-ha̍k siá chò mathematics, kán-siá chò maths (Liân-pang Eng-gí), math (Bí-kok Eng-gí).
Sò͘-ha̍k ê le̍k-sú[siu-kái | kái goân-sí-bé]
Sò͘-ha̍k ê ián-piàn ē-tit khoàⁿ chò kóng thiu-siōng ê chú-tê iah sī thêng-tō͘ ti̍t-ti̍t leh cheng-ka. Siōng chá ê thiu-siōng hoān-sè sī sò͘-ba̍k. Liáu-kái kóng 2 lia̍p phōng-kó kap 2 lia̍p kam-á ká-ná ū siáⁿ-mih sio-kâng ê só͘-chāi, sò͘-ha̍k tō khai-sí hoat-tián--a.
Sú-chêng ê jîn-lūi ē-hiáu sǹg kū-thé ê mi̍h-kiāⁿ, mā chai-iáⁿ beh án-choáⁿ sǹg thiu-siōng ê sò͘-liōng, chhiūⁿ kóng sî-kan (kang, kùi, nî, ...). Ē-hiáu sǹg, koh lâi tō sī sǹg-siàu (chhiūⁿ ke, kiám, sêng, tû).
M̄-koh beh sǹg tio̍h-ài ē-tàng siá kap 1 thò sò͘-jī hē-thóng. Sú-chêng ê jîn-lūi hoān-sè sī tī thô͘-kha oē sûn iah sī tī chhâ-thaû khek sûn lâi piáu-sī sò͘-liōng. Inca Tè-kok bô su-siá hē-thóng, in lī-iōng soh-á phah-kat ê hong-hoat lâi sǹg-siàu, hō-chò khipu.
Sò͘-ha̍k ê hoat-tián kap chhek-liông thó͘-tē, chhú-lí koè-kè, ī-chhek thian-bûn sū-kiāⁿ ū chin bi̍t-chhiat ê koan-hē. In-ūi ū su-iàu, sò͘-ha̍k lāi-té chhú-lí khong-kan, kiat-kò͘, piàn-tōng ê gián-kiù tō toè leh hoat-tián. Khah lō͘-boé, beh kái-koat sio kap kng ê bûn-tê, sò͘-ha̍k bu̍t-lí-ha̍k mā khai-sí hoat-tián.
Tû-khì éng-koè chiah-ê gián-kiù ê chú-tê, sò͘-ha̍k kaù taⁿ mā iû-goân it-ti̍t leh chhòng-sin.
Sûn sò͘-ha̍k kap èng-iōng sò͘-ha̍k[siu-kái | kái goân-sí-bé]
Ū oh kái-koat ê būn-tê tō su-iàu sò͘-ha̍k. Éng-koè chhiūⁿ siong-gia̍p, thó͘-tē chhek-liông, thian-bûn-ha̍k; hiān-chhú-sî toā-pō͘-hūn ùi chū-jiân kho-ha̍k tit tio̍h lêng-kám, chiâⁿ chē sò͘-ha̍k-ka mā sī bu̍t-lí-ha̍k-ka. Chhiūⁿ í-chá Newton hoat-tián bî-chek-hun, Richard Feynman hoat-tián Feynman kèng-chek-hun, chit-má thaù-koè chhui-lí kap tùi bu̍t-lí ê chhim-ji̍p liáu-kái, tō hoat-tián chhut hiân-lūn (string theory).
Ū būn-tê beh kái-koat, gián-kiù siong-koan ê sò͘-ha̍k liáu-aū, tō ē-tit it-ti̍t èng-iōng chiah-ê sò͘-ha̍k. Kā ū kiōng-tông ki-chhó͘ ê sò͘-ha̍k khioh chò-hoé, chi̍t-koá koan-liām ē-tit tha̍h chò-hoé. 19 sè-kí ê sî, tō án-ne kā sò͘-ha̍k hun-chò èng-iōng sò͘-ha̍k kap sûn sò͘-ha̍k.
Sò͘-ha̍k hō͘ lâng kám-kak iu-ngá, hoān-sè i ê pún-chit tō sī bí-ha̍k, hoān-sè i pun-sin ū 1 chióng bí-kám, m̄-koh che lóng chin oh bêng-khak piáu-ta̍t. Kán-tan-sèng kap phó͘-phiàn-sèng sī sò͘-ha̍k 2 ê chin tiong-iàu ê te̍k-sek. Chiah-ê khoàⁿ--khí-lâi taù bē chò-hoé ê sèng-chit ū-tang-sî-á ē-tàng kiat-ha̍p, chhiūⁿ kóng kā chi̍t-koá bô kāng hun-ki ê sò͘-ha̍k it-thé-hoà, iah sī hoat-tián ē-sái kiōng-tông kè-sǹg ê ke-si. Sûn sò͘-ha̍k chho͘-chho͘ khoàⁿ ká-ná kan-taⁿ i ê bí-kám ū koá kè-ta̍t, kan-taⁿ sò͘-ha̍k-ka ū chhù-bī. M̄-koh gián-kiù chi̍t-ē chìn-tián liáu-aū, sûn sò͘-ha̍k tiāⁿ ē pìⁿ-chiâⁿ èng-iōng sò͘-ha̍k.
Sò͘-ha̍k hû-hō[siu-kái | kái goân-sí-bé]
Sò͘-ha̍k ê bûn-chiuⁿ bô kài hó tha̍k. Stephen Hawking 1988 chhut ê Sî-kan kán-sú (A Brief History of Time) lāi-té kan-taⁿ ū 1 tiâu sò͘-ha̍k kong-sek, in-ūi chhut-pán-siong kóng múi 1 tiâu kong-sek tō ē kā siau-lō͘ kàng chi̍t-poàⁿ.
Sò͘-ha̍k-ka chin giâm-keh iau-kiû ài kā siuⁿ beh piáu-ta̍t--ê siá chheng-chhó, chóng--sī sò͘-ha̍k iáu-sī ká-ná hoat-lu̍t tiâu-bûn hiah pháiⁿ tha̍k. Sò͘-ha̍k-ka khok-chhiong chū-jiân gí-giân, ēng tēng kah chin bêng-khak ê sò͘-ha̍k bêng-sû, sò͘-ha̍k hû-hō kap bûn-hoat (gí-hoat) lâi ta̍t kaù giâm-keh ê bo̍k-phiau. Ū chi̍t-koá bêng-sû chioh ēng phó͘-thong ê bêng-sû, m̄-koh ì-sù bô tī-tāi, chhiūⁿ khoân (ring), kûn (group), lūi (category); ū-ê bêng-sû sī sò͘-ha̍k choan-iōng--ê, chhiūⁿ homotopy, Hilbert khong-kan. Thiaⁿ kóng Henri Poincaré hông soán ji̍p-khì Hoat-kok Gián-kiù-īⁿ (Académie Française) tō sī beh chhiáⁿ i lâi tēng-gī automorphe.
Sò͘-ha̍k kap kho-ha̍k[siu-kái | kái goân-sí-bé]
Carl Friedrich Gauss kóng sò͘-ha̍k sī kho-ha̍k ê lú-ông. Sò͘-ha̍k bu̍t-lí-ha̍k-ka Leon M. Lederman khau-sé kóng bu̍t-lí-ha̍k-ka kan-taⁿ sūn-thàn sò͘-ha̍k-ka, sò͘-ha̍k-ka kan-taⁿ sūn-thàn Siōng-tè, sui-bóng chiah-nī kò͘-khiam ê sò͘-ha̍k-ka chin oh chhoē.
Sò͘-ha̍k gián-kiù ê hoān-ûi[siu-kái | kái goân-sí-bé]
Chá-kî ê sò͘-ha̍k ūi tio̍h siong-gia̍p, chhek-liông, ī-chhek thian-bûn hiān-siōng, hoat-tián kiat-kò͘, khong-kan, piàn-tōng ê gián-kiù, chhiūⁿ tāi-sò͘ (algebra), kí-hô-ha̍k (geometry), hun-sek (analysis). Aū--lâi, tau̍h-tau̍h koh hoat-tián kaù lô-chek, khah kán-tan ê ki-chhó͘ hē-thóng (foundations), kap khah si̍t-iōng ê èng-iōng sò͘-ha̍k (applied mathematics).
Sò͘-ha̍k chú-iàu ê gián-kiù[siu-kái | kái goân-sí-bé]
Chia lia̍t--ê sī khah chú-iàu ê gián-kiù tê-ba̍k. Khah oân-chéng ê gián-kiù chú-tê chhiáⁿ chham-khó sò͘-ha̍k chú-tê lia̍t-toaⁿ.
Sò͘-liōng (Quantity)[siu-kái | kái goân-sí-bé]
Leh chhú-lí sò͘-ba̍k, chi̍p-ha̍p, toā-sè (size) chit lūi ê būn-tê, kap chaú-chhoē chhú-lí ê hong-hoat.
- Sò͘-ba̍k – Chū-jiân-sò͘ – Chéng-sò͘ – pí-sò͘ – Si̍t-sò͘ – Ho̍k-cha̍p-sò͘ – Hypercomplex numbers – Quaternions – Octonions – Sedenions – Hyperreal numbers – Surreal numbers – Ordinal numbers – Cardinal numbers – p-adic numbers – Integer sequences – Sò͘-ha̍k tiāⁿ-sò͘ – Number names – Bû-hān – ki-té (Base)]]
Piàn-tōng (Change)[siu-kái | kái goân-sí-bé]
Leh chhú-lí sò͘-ba̍k kap hâm-sò͘ ê piàn-hoà.


Sǹg-siàu (Arithmetic) Bî-chek-hun Hiòng-liōng bî-chek-hun Hun-sek (Analysis) 

Bî-hun hong-têng (Differential equations) Tōng-thài hē-thóng (Dynamical systems) Hūn-tūn lí-lūn (Chaos theory)
- Sǹg-siàu (Arithmetic) – Bî-chek-hun – Hiòng-liōng bî-chek-hun – Hun-sek (Analysis) – Bî-hun hong-têng (Differential equations) – Tōng-thài hē-thóng (Dynamical systems) – Hūn-tūn lí-lūn (Chaos theory) – Hâm-sò͘ lia̍t-toaⁿ
Kiat-kò͘ (Structure)[siu-kái | kái goân-sí-bé]
Leh chhú-lí toā-sè (size), tùi-thīn (symmetry) kap chi̍t-koá sò͘-ha̍k kiat-kò͘ (mathematical structure) ê būn-tê.


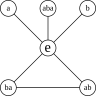
Thiu-siōng tāi-sò͘ Sò͘-lūn Kûn-lūn (Group theory) 


Topology Category theory Order theory
- Thiu-siōng tāi-sò͘ – Sò͘-lūn – Tāi-sò͘ kí-hô-ha̍k – Kûn-lūn (Group theory) – Monoids – Hun-sek (Analysis) – Topology – Soàⁿ-sèng tāi-sò͘ (Linear algebra) – Tô͘-lūn (Graph theory) – Universal tāi-sò͘ (Universal algebra) – Category theory – Order theory – Measure theory
Khong-kan koan-hē (Spatial relations)[siu-kái | kái goân-sí-bé]
Ē-tàng khoàⁿ ê sò͘-ha̍k.


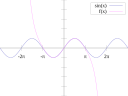


Topology Kí-hô-ha̍k Saⁿ-kak-hoat Bî-hun kí-hô-ha̍k Chhùi-hêng kí-hô-ha̍k (Fractal geometry)
- Topology – Kí-hô-ha̍k – Saⁿ-kak-hoat – Tāi-sò͘ kí-hô-ha̍k – Bî-hun kí-hô-ha̍k – Bî-hun topology (Differential topology) – Tāi-sò͘ topology (Algebraic topology) – Soàⁿ-sèng tāi-sò͘ – Chhùi-hêng kí-hô-ha̍k (Fractal geometry)
lî-sàn sò͘-ha̍k (Discrete mathematics)[siu-kái | kái goân-sí-bé]
Leh chhú-lí kan-taⁿ ē-tàng 1 ê 1 ê sǹg ê mi̍h-á.
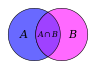
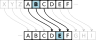

Combinatorics Native chi̍p-ha̍p-lūn (Naive set theory) Kè-sǹg lí-lūn (Theory of computation) Bi̍t-bé-ha̍k (Cryptography) Tô͘-lūn (Graph theory)
- Combinatorics – Native chi̍p-ha̍p-lūn (Naive set theory) – Kè-sǹg lí-lūn (Theory of computation) – Bi̍t-bé-ha̍k (Cryptography) – Tô͘-lūn (Graph theory)
Èng-iōng sò͘-ha̍k (Applied mathematics)[siu-kái | kái goân-sí-bé]
Leh kái-koat hiān-si̍t būn-tê ê sò͘-ha̍k.
- Sò͘-ha̍k bu̍t-lí-ha̍k (Mathematical physics) – Mechanics – Fluid mechanics – Numerical analysis – Optimization – Ki-lu̍t – Thóng-kè-ha̍k – Financial mathematics – Game theory – Mathematical biology – Bi̍t-bé-ha̍k (Cryptography) – Chu-sìn lí-lūn (Information theory)
Tēng-lí (Theorems)[siu-kái | kái goân-sí-bé]
Che lia̍t chi̍t-koá m̄-sī sò͘-ha̍k-ka mā ē kám-kak sim-sek ê tēng-lí. Oân-chéng ê chu-liāu chhiáⁿ chham-khó Tēng-lí lia̍t-toaⁿ.
- Ti̍t-kak tēng-lí (Pythagorean theorem) – Fermat choè-aū tēng-lí (Fermat's last theorem) – Gödel's incompleteness theorems – Cantor's diagonal argument – 4 sek tēng-lí (Four color theorem) – Zorn's lemma – Euler's identity – Church-Turing thesis– Riemann hypothesis – Continuum hypothesis – Central limit theorem – Sǹg-siàu ki-pún tēng-lí (Fundamental theorem of arithmetic) – Tāi-sò͘ ki-pún tēng-lí (Fundamental theorem of algebra) – Bî-chek-hun ki-pún tēng-lí (Fundamental theorem of calculus) – Fundamental theorem of projective geometry – Gauss-Bonnet theorem.
Chhai-chhek (Conjectures)[siu-kái | kái goân-sí-bé]
Che lia̍t chi̍t-koá tng-leh gián-kiù ê būn-tê. Oân-chéng ê chu-liāu chhiáⁿ chham-khó Chhai-chhek lia̍t-toaⁿ.
- Goldbach Chhai-chhek – Twin prime conjecture – Collatz conjecture – Poincaré conjecture – classification theorems of surfaces – P=NP
Lēng-goā, ū-ê sò͘-ha̍k-ka jīn-ûi continuum hypothesis kap ZFC bô tī-tāi, bián chhap i; ū-ê khah chek-ke̍k leh gián-kiù.
Ki-chân kap hong-hoat (Foundations and methods)[siu-kái | kái goân-sí-bé]
Leh su-khó sò͘-ha̍k ê pún-chit kap sò͘-ha̍k beh án-choáⁿ gián-kiù.
- Philosophy of mathematics – Mathematical intuitionism – Mathematical constructivism – Sò͘-ha̍k ê ki-chân (Foundations of mathematics) – Chi̍p-ha̍p-lūn – Hû-hō lô-chek (Symbolic logic) – Bô͘-hêng-lūn (Model theory) – Category theory – Lô-chek – Reverse Mathematics – Sò͘-ha̍k hû-hō-pió (Table of mathematical symbols)
Sò͘-ha̍k-sú kap sò͘-ha̍k-ka[siu-kái | kái goân-sí-bé]
Chhiáⁿ chham-khó sò͘-ha̍k-sú lia̍t-toaⁿ
- Sò͘-ha̍k-sú – Sò͘-ha̍k nî-pió – Sò͘-ha̍k-ka – Fields Chióng – Abel Prize – Millennium Prize Problems (Clay Math Prize) – International Mathematical Union – Mathematics competitions – Lateral thinking – Mathematical abilities and gender issues
Sò͘-ha̍k ê hûn-iáⁿ[siu-kái | kái goân-sí-bé]
Tùi sò͘-ha̍k ê gō͘-kái[siu-kái | kái goân-sí-bé]
Sò͘-ha̍k m̄ sī 1 ê sím-mih būn-tê lóng kái-koat tiāu ê hē-thóng, i lāi-té iáu chin chē ài gián-kiù ê būn-tê.
Ké-sò͘-ha̍k khoàⁿ--khí-lâi chhin-chhiūⁿ sò͘-ha̍k, i bô tī ha̍k-su̍t-kài chiap-siū kàm-tok, ū-sî-á koh si sò͘-ha̍k-ka pìⁿ--ê. I thong-siông sī leh thó-lūn khah ū-miâ ê būn-tê, m̄-koh i koh m̄ sī ēng lâng chèng-bêng koè ê lí-lūn chò ki-chân lâi chèng-bêng. Ké-sò͘-ha̍k kap sò͘-ha̍k tō ká-ná ké-kho-ha̍k kap kho-ha̍k chhan-chhiūⁿ. Chit khoán tāi-chì ē lâi hoat-seng ê goân-in ū:
- bô hù-ha̍p giâm-keh ê iau-kiû;
- in-ūi bó͘ chi̍t-koá in-sò͘, bô chun-chiàu sò͘-ha̍k lūn-bûn ài seng keng-koè tông-liâu sím-cha, tī ha̍k-su̍t kî-khan hoat-piáu, ... chiah-ê têng-sū;
- tùi bûn-hiàn bô kài liáu-kái.
Chham-khó[siu-kái | kái goân-sí-bé]
- Benson, Donald C., The Moment of Proof: Mathematical Epiphanies, Oxford University Press, USA; New Ed edition (December 14, 2000). ISBN 0-19-513919-4.
- Boyer, Carl B., A History of Mathematics, Wiley; 2 edition (March 6, 1991). ISBN 0-471-54397-7. — A concise history of mathematics from the Concept of Number to contemporary Mathematics.
- Courant, R. and H. Robbins, What Is Mathematics? : An Elementary Approach to Ideas and Methods, Oxford University Press, USA; 2 edition (July 18, 1996). ISBN 0-19-510519-2.
- Davis, Philip J. and Hersh, Reuben, The Mathematical Experience. Mariner Books; Reprint edition (January 14, 1999). ISBN 0-395-92968-7.— A gentle introduction to the world of mathematics.
- Eves, Howard, An Introduction to the History of Mathematics, Sixth Edition, Saunders, 1990, ISBN 0-03-029558-0.
- Gullberg, Jan, Mathematics—From the Birth of Numbers. W. W. Norton & Company; 1st edition (October 1997). ISBN 0-393-04002-X. — An encyclopedic overview of mathematics presented in clear, simple language.
expanded version of a Soviet mathematics encyclopedia, in ten (expensive) volumes, the most complete and authoritative work available. Also in paperback and on CD-ROM, and online [1].
- Jourdain, Philip E. B., The Nature of Mathematics, in The World of Mathematics, James R. Newman, editor, Dover, 2003, ISBN 0-486-43268-8.
- Kline, Morris, Mathematical Thought from Ancient to Modern Times, Oxford University Press, USA; Paperback edition (March 1, 1990). ISBN 0-19-506135-7.
- Monastyrsky, Michael (2001). "Some Trends in Modern Mathematics and the Fields Medal" (PDF). Canadian Mathematical Society. 2006-07-28 khòaⁿ--ê.
- The Oxford Dictionary of English Etymology, 1983 reprint. ISBN 0-19-861112-9.
- Pappas, Theoni, The Joy Of Mathematics, Wide World Publishing; Revised edition (June 1989). ISBN 0-933174-65-9.
- Peterson, Ivars, Mathematical Tourist, New and Updated Snapshots of Modern Mathematics, Owl Books, 2001, ISBN 0-8050-7159-8.
- Pang-bô͘:Cite book en
- Pang-bô͘:Cite journal en
- Pang-bô͘:Cite journal en
- Pang-bô͘:Cite book en
- Ziman, J.M., F.R.S. (1968). "Public Knowledge:An essay concerning the social dimension of science".
| |||||||||||||||||||






















![{\displaystyle [1,2,3][1,3,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3456de48f67f15147542c745a3a8cbe64d9ed7e)
![{\displaystyle [2,1,3][2,3,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2982b802b037da0f46b428d63581818291e5a8bd)
![{\displaystyle [3,1,2][3,2,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fd3d1378424e83c7f56eef8db2ea044b149c25a)


